[논문요약] DLinear, NLinear ( LTSF-Linear ) 리뷰

Are Transformers Effective for Time Series Forecasting?

Abstract

• 원문 바로가기

<기존 방법의 한계점>

논문은 다음과 같은 질문에서 시작합니다.

시계열 예측에 Transformer기반 모형을 적용하는게 정말 효과적일까?

• transformer를 활용한 LTSF(long-term series forecasting)에 관현 연구가 지난 몇년 간 좋은 성과를 보였습니다.
• transforemr는 긴 시퀀스 사이에 semantic(의미론적) 상관관계를 추출하는데 가장 성공적인 방법인 것은 맞지만, 시간적 관계를 추출해야하는 시계열 예측 모델링에선 아래와 같은 이유로 단점이 존재합니다.
  • transformer가 순서가 있는 정보를 저장하는 것을 가능하게 하기 위해
  • positional encoding과 sub-series 임베딩된 토큰을 사용하는 동안 permutation-invariant self-attention 매커니즘은 불가피하게 시간적 정보가 손실됩니다.
• 이 논문에선 Transformer기반 TSF solution이 타당한지 의문을 제기하고자 합니다.
• Transformer 기반 논문에선 비교 모델로 주로 자기회귀적인 예측 솔루션을 사용했는데 이것들은 error accumulation effects를 피할 수 없기 때문에 long-term 예측에선 성능이 안좋을 수 밖에 없습니다.

<논문의 해결책>

• 논문에선 LTSF-Linear라는 정말 간단한 아키텍처를 사용한 모델을 제시합니다.
  • DLinear는 시계열 데이터를 trend와 remainder 두개로 분해하고, 두개의 one-layer networks를 사용하여 두개의 시리즈를 모델링해 예측을 수행합니다.

<실험 내용 및 결과>

• 거의 모든 케이스에서 LTSF-Linear가 Transformers모델보다 좋은 성능을 보이는 것을 확인하였습니다.
• 또한 다양한 디자인의 LTSF 모델의 효과를 탐구하였습니다.

 

 

Introduction

<가설>

• 장기 예측은 추세와 주기성이 뚜렷한 시계열에서만 가능하다는 가설을 세움

<결과>

따라서 본 논문에서는

1.밴치마크데이터셋 9개에서 transformer모델보다 outperform한 것을 확인하였습니다.

2.대부분의 transformer모델이 긴 시퀀스에서 시간적 관계를 추출하는것에 실패 했음을 확인하였습니다.

3. Transformer기반 TSF에 다양한 디자인 요소가 미치는 영향을 연구하였습니다.

• 논문에서는 긴 입력을 모델링 하는 것에서 부터, 시계열 순서에 대한 민감도, positional encoding의 영향, 하위시리즈 임베딩, 효율성을 비교합니다.

 

Preliminaries : TSF Problem Formulation

아래와 같은 C개의 historical data가 있을때

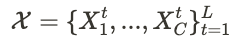
L : look-back window

x_i^t : t time step에서 i번째 원소

이때, 예측하고자하는 T future time steps는 다음과 같이 표현할 수 있습니다.

 

IMS(iterated multi-step)	DMS(direct multi-step)
single step forcaster를 학습하여 multi-step 예측을 얻기 위해 반복적으로 적용	직접적으로 multi-step을 한번에 최적화
상대적으로 분산이 작다. (autoregressive estimation 때문에)
single-step에서 높은 정확도	unbiased 한 single step 모델을 얻기 어려울 때 높은 정확도
T가 상대적으로 작을 때	T가 상대적으로 클 때
error accumulation effect 문제가 있을 수 있음
RNN-based TSF , traditional-statistical model	LTSF-Linear

• CNN이나 transformer 기반 방법은 Encoder와 Decoder에 따라 IMS or DMS

 

An Embarrassingly Simple Baseline

<가설>

• 존재하는 Transformer-based LTSF 연구에서 비교되는 non-Transforemer 모델은 대부분 IMS forecasting이고, 이것은 error accumulation effects의 문제가 있습니다.
• 이 논문에서는 성능 향상이 대부분 DMS strategy 때문이라고 가정합니다.
• 이 가설을 검증하기 위해 시간적 선형 레이어를 통해 가장 간단한 DMS, LTSF-Linear 를 제시합니다.
•  

 

두가지 LTSF-Linear모델이 있습니다.

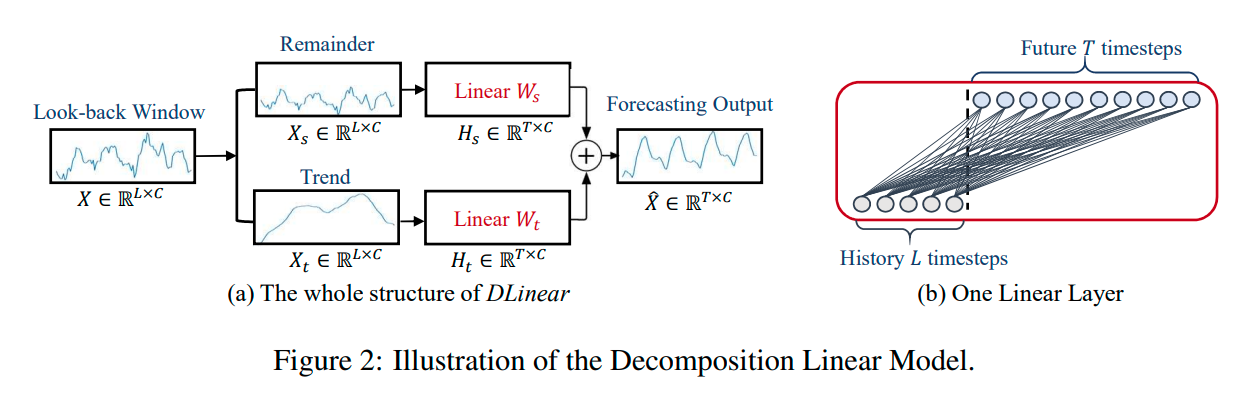
DLinear

• Autoformer와 FEDformer에 사용되는 분해 방식의 조합입니다.
• raw data를 이동평균으로 trend 성분과 remainder(seasonal) 성분으로 분해하고, 최종적으로 예측을 얻기 위해 두 성분을 합합니다.
• trend를 명시적으로 처리하기 위해, DLinear는 data에서 추세가 명확할 때 vanilla Lnear의 성능이 향상됩니다.
  • Vanilla Linear : one layer linear model

(1) X^=Hs​+Ht​
(2) Remainder Hs​=Ws​Xs​
(3) Trend Ht​=Wt​Xt​

 

 

NLinear

• LTSF-Linear의 성능을 향상시키기 위해 데이터의 분포이동이 있을 때, NLinear는 먼저 마지막 시퀀스만큼 인풋을 뺍니다.
• 그런 다음 선형 레이어를 통과하고, 뺀 부분 만큼 마지막 prediction을 하기 전에 다시 합합니다.
• 이 NLinear에서 subtraction과 addition는 시퀀스 인풋을 위한 정규화

 

 

 

The Features of LTSF-Linear

• An O(1) maximum signal traversing path length
  • path가 짧을 수록 의존성이 더 잘 포착되어 긴 범위와 짧은 범위의 temporal relation을 최대 O(1)로 둘 다 잘 포착할 수 있습니다.
• High-efficiency
  • 최대 두 개의 layer를 사용하므로 낮은 메모리와 적은 파라미터를 사용해 존재하는 Transformer보다 빠른 추론이 가능합니다.
• Interpretability
  • 훈련 후에 예측값에 대한 인사이트를 얻기 위해 계절성과 추세 분기로부터 가중치를 시각화 할 수 있습니다.
• Easy-to-use
  • hyper-parameter튜닝 없이 쉽게 사용할 수 있습니다.

 

Transformer-Based LTSF Solutions

 

• Time series decomposition
  • moving average kernel을 사용해 데이터를 좀더 예측하기 쉽도록 trend-cyclical component와 seasonal component로 분해하는 기법입니다.
  • Autoformer, FEDformer에서 다양한 크기의 Kernel을 통해 시계열 분해 구조를 도입하였습니다.
• Input Embedding Strategies
  • Transformer의 Self-Attemtion Layer는 Positional Information을 보존하지 못하기 때문에 fixed positional encoding, a channel projection embedding, learnable temporal embeddings, temporal embeddings with a temporal convolution layer, learnable timestamps 같은 임베딩 방법을 사용합니다.
• Self-Attention Schemes
  • Semantic Dependency를 추출하기 위해 self-attention mechanism에 의존하는데 vanilla transformer는 O(L^2)로 시간복잡도와 메모리 복잡도가 큽니다.
  • 시간 복잡도를 줄이기 위해 Pyraformer는 pyramidal attention를, informer는 a ProbSparse self-mechanism을 사용함. Autoformer는 auto-correlation mechanism을 사용해 self-attention layer를 대체합니다.
• Decoder
  • vanilla Transformer decoder는 autoregressive한 방식으로 아웃풋 시퀀스가 나오기 때문에 특히, long-term prediction에서 느린 추론속도와 error accumulation effect가 발생합니다.
  • 여러 모델에서 이 문제를 해결하기 위해 다양한 방식을 활용합니다.
  • Informer는 DMS forecasting으로 decoder를 디자인합니다. Pyraformer는 시공간이 연결된 완전 연결 레이어 축을 디코더로 사용합니다. Autoformer는 trend 요소와 계절 요소를 위해 축척된 자기상관 매커니즘 두개의 분해된 특징을 합합니다. FEDformer도 분해된 스키마를 사용합니다.

 

 

efficiency

 

• window size 96으로 720 timstep을 예측했을 때 DLinear가 파라미터 수가 가장 적어 시간복잡도, 메모리, 파라미터가 같은 transformer 모델 보다 시간과 메모리 측면에서 이점을 얻는 것을 확인할 수 있습니다.

 

Look-back Windows

• look-back window size가 커짐에 따라 LTSF-Linear의 성능이 대부분의 데이터에 대해 유의미하게 향상되었습니다.
• but, 금융데이터에 대해서는 노이즈 때문에 입력의 길이가 늘어날 수록 악화된 결과를 보였습니다.
• transformer모델에 대해서는 window size가 커짐에 따라 성능이 변동하거나 악화되었습니다.

 

 

Experiments

Experimental Settings

• Evaluation metric
  • MSE
  • MAE
• Compared methods
  • Transformer-based methods
    • FEDformer
    • Autoformer
    • Informer
    • Pyraformer
    • LogTrans
  • naive DMS method
    • Closet Repeat : 마지막 look-back window에있는 값을 반복하는 것

Comparison with Transformers

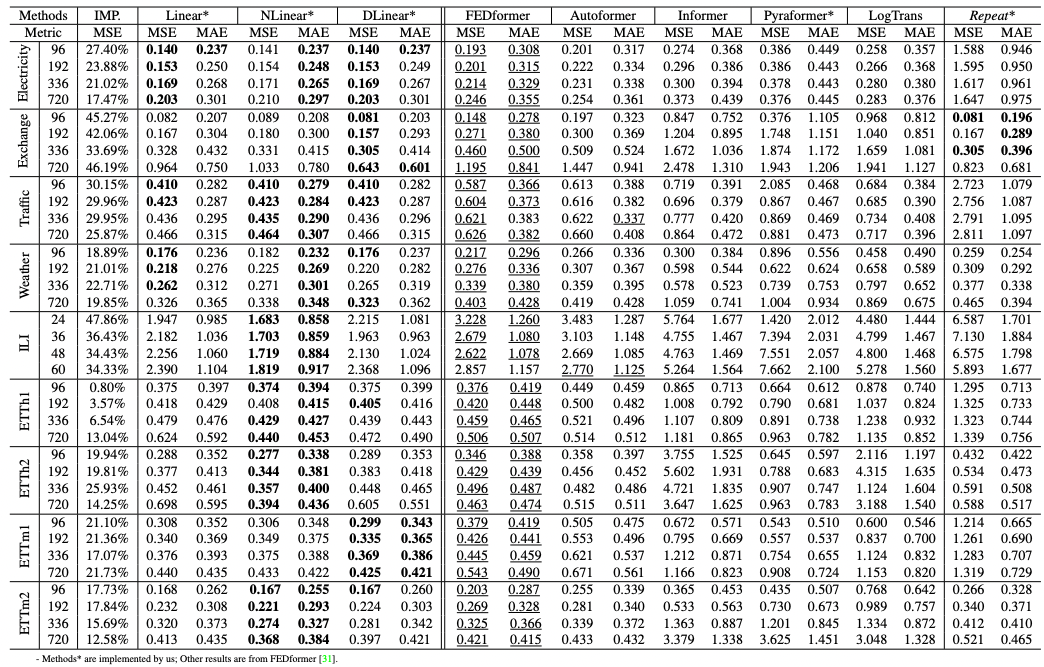
• Quantitative results
  • LTSF-Linear모델이 다변량 시계열에서 SOTA FEDformer모델을 대부분의 케이스에서 20~50% 능가하였습니다.
  • 단변량 시계열에서도 Transformer기반 모델에 비해 LTSF-Linear 모델이 우수한 성능을 보였습니다.
  • NLinear와 DLinear는 데이터 분포 변화와 추세-시계열 특징을 처리하는데 우수성을 보였습니다.

 

 

Interpretability

 

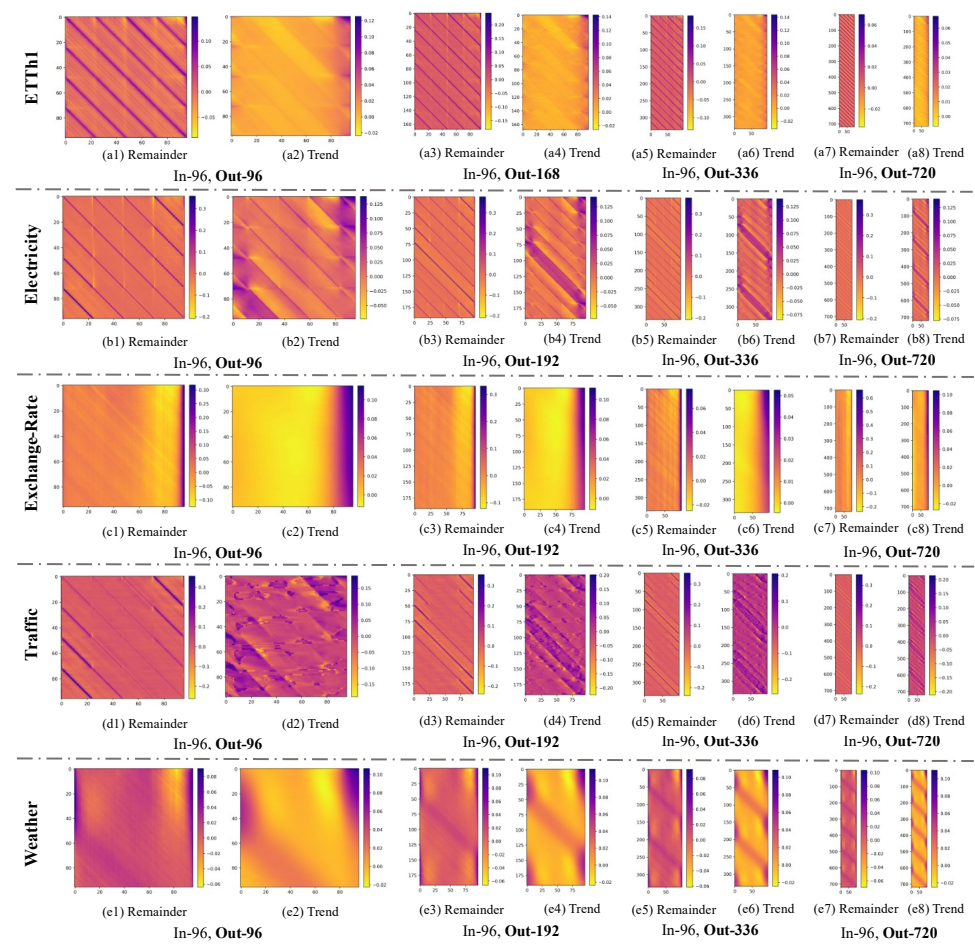
• 예측값에 대해 추세와 계절성에 대한 가중치를 시각화하여 해석할 수 있습니다.
• ETTh1, Electricity, Traffic의 경우 24step의 주기로 패턴이 반복되는 것을 볼 수 있는데 하루단위로 계절성이 존재하는 것을 확인할 수 있습니다.
• Exchange-Rate의 경우 금융데이터의 특성상 주기성과 계절성이 거의 존재하지 않아 일정한 패턴이 나타나지 않지만, Trend Layer를 통해 Output에 가까운 정보들이 높은 Weight를 가지고 있는 것을 보며, 해당 데이터들이 예측값에 많은 기여를 하고 있음을 확인할 수 있습니다.

 

Conclusion

• 간단한 선형모델을 사용하는 것이 오히려 Transformer기반 모형보다 나을 수 있습니다.
• 본 논문은 기존 선형모형에 흐름에서 진행된 연구가 아닙니다. informer같은 모형이 Best paper로 채택되는 연구의 흐름 속에서 Transformer를 시계열 예측에 사용하는 방향에 대해 근본적인 질문을 던집니다.

 

Future work

• LTSF-Linear모형은 굉장히 간단하지만 해석가능하다는 점에서 강점을 가집니다.
• 이 잠재성이 새로운 모델을 디자인하거나 전처리하는데 중요한 포인트가 될 수 있습니다.